Differentiation Applications

Home Review Practice Tests Homework Assignments

 

 

  Home

3.1 to 3.6 Differentiation Applications

Download as Word Document

Practice Test: No Calculators Permitted on Parts A-L                                                                  

A. For the labeled points on the graphs below, decide whether each is an absolute maximum or minimum, a relative maximum or minimum, or neither (5 points each)

1.

 
D
D
E
A
A

2.

C
B
B
C
a
E

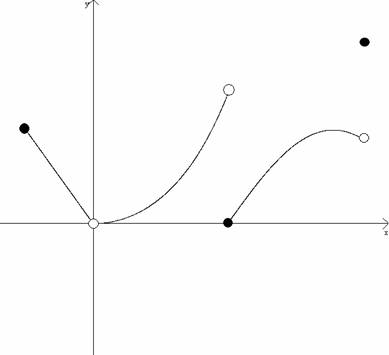
B. Determine the critical numbers of the function (3 points each).

3.                                                       4.

 

5.                                                         6.

C. Determine the absolute maximum and minimum of the function on the designated closed interval (5 points each).  

7.                                      8.

9.                            10.

11.                                12.          

13.                                 14.

D. Determine all absolute extrema of the function (if any) that exist over each interval (8 points).

15.

a.                                                                   b.

c.                                                                   d.

E. Determine if Rolle’s Theorem can be applied to  f  on the closed interval [a,b]. If Rolle’s Theorem can be applied, find all values c, a<c<b, for which  (2-4 points each).

16.                               17.

18.                                       19.

F. Determine if the Mean Value Theorem can be applied to  f  on the closed interval [a,b]. If it can be applied, find all values c, a<c<b, for which  (2-5 points each).

20.                              21.

22.                                           23.

24.                                        25.

G. A graph of a function  f  is drawn on the closed interval . Determine if the Mean Value Theorem applies to  f  on the interval , and if so, draw the tangent line that passes through the point  c for which the instantaneous rate of change is equal to the average rate of change of  f on . If the Mean Value Theorem does not apply to  f , explain why. (4 points each)

26.

 

 

 

 

 

 

a

 

27.
b

 

 

 

 

 

 

 

b

 

H. Use the First Derivative Test to find all relative extrema of  f (5 points each).

28.                                               29.

30.                                     31.

I. Use the Second Derivative Test to find all relative extrema of  f (5 points each).

32.                               33.

J. For each function  f  shown below, a) Find the critical numbers of  f, b) Determine all relative extrema of  f, c) Determine the intervals on which  f  is increasing or decreasing, and d) Determine the intervals on which  f  is concave up or down (10 points each).

34.                                               35.

36.                                                       37.

K. The graph of  f  is shown. Label all points of inflection of the graph of  f (3 points each).

38.                                                                                                                                                              39.

 

 

 

 

 

 

 

L. Graph the function . Identify all of the items listed below and be sure that they are reflected in your graph (20 points):
bulletDomain
bulletx-intercepts
bullety-intercepts
bulletCritical numbers of  f
bulletRelative extrema of  f
bulletIntervals of increase/decrease for  f
bulletPoints of Inflection of  f
bulletConcavity of  f  (Intervals of Concave Up/Down)
bulletVertical Asymptotes of  f
bulletHorizontal Asymptotes of  f

M. Use problem solving strategies to complete the problem. A calculator is permitted/required on this part of the examination.

41. An unfathomably strong man throws a wrench upwards from the top of a 200 m cliff at an initial velocity of 45 . The height of the wrench, s, measured in meters, can be modeled as a function of time, t, measured in seconds, by the following position function:

(a)    Find an equation for  v(t), the velocity of the wrench as a function of time  t. (2 points)

(b)    Find the velocity of the wrench at time 4. Indicate units of measure. (2 points)

(c)    Is the wrench moving upwards or downwards at time ? Justify your answer. (2 points)

(d)    Find the average velocity of the wrench from time  to the time at which it impacted the ground. Indicate units of measure. (4 points)

(e)    Find the time  t  for which the instantaneous velocity is equal to the average velocity found in part (d). (4 points)

(f)      Find the total distance traveled by the wrench from  to the time at which it impacted the ground. Indicate units of measure. (6 points)

Scoring Guidelines

A: 173-230                              (You would receive a “5” if this were an AP Exam)

B: 140-172                              (You would receive a “4” if this were an AP Exam)

C: 115-139                              (You would receive a “3” if this were an AP Exam)

D: 83-114                               (You would receive a “2” if this were an AP Exam)

F: 0-83                                    (You would receive a “1” if this were an AP Exam)

How to Calculate your Score:

  1. Use the solutions guide to determine which problems you got incorrect or at least partially incorrect.
  2. Use the scoring guidelines to determine how many points you would lose for each of your incorrect answers.
  3. Add up the number of lost points and subtract them from 230. This is your raw score.
  4. Convert your raw score to a letter grade.

Points Lost:

A.                                                        G.                                                        M.                               

B.                                                         H.                               

C.                                                        I.                                 

D.                                                        J.                                 

E.                                                         K.                               

F.                                                         L.                                

Total Points Lost:                                         

Raw Score:                                                    

Letter Grade:                                                

SCORING GUIDELINES

A.           Objective: Recognize maxima and minima in the graphs of functions

·         (1) Point will be awarded for each correctly identified point on the graph. An incorrectly identified point will result in no credit.

B.      Objective: Be able to find the critical numbers of a function

·         (1) Point will be awarded for finding the derivative of the function.

·         (1) Point will be awarded for setting the derivative equal to zero and/or finding where it might be undefined.

·         (1) Point will be awarded for correctly identifying all critical numbers. If not all critical numbers are correctly listed but at least one is correctly listed, (1/2) of a point will be earned.

C.      Objective: Be able to apply critical numbers of a function to find global maxima and minima on a closed interval.

·         (1) Point will be awarded for finding the derivative of the function.

·         (1) Point will be awarded for finding the critical numbers of the function.

·         (1) Point will be earned for testing the function at the critical numbers and the endpoints.

·         (1) Point will be earned for correctly identifying the global maximum on the closed interval.

·         (1) Point will be earned for correctly identifying the global minimum on the closed interval.

D.     Objective: Understand the ability (or lack there of) of maxima and minima to exist on different types of intervals.

·       (2) Points will be awarded for determining the critical numbers of the function. (1) point will be awarded if only one critical number is identified correctly.

·       (2) Points will be awarded for evaluating the function at the interval endpoints and at the critical numbers.

·       (1) point will be awarded for each correct answer to (a), (b), (c), and (d).

E.      Objective: Understand Rolle’s Theorem and the conditions under which it applies.

            If Rolle’s Theorem DOES NOT APPLY:

·        (1) Point will be awarded for correctly identifying that Rolle’s Theorem does not apply.

·        (1) Point will be awarded for proper mathematical work or a correct explanation that explains why Rolle’s Theorem does not apply.

If Rolle’s Theorem DOES APPLY:

·        (1) Point will be awarded for correctly identifying that Rolle’s Theorem does apply.

·        (1) Point will be awarded for finding the derivative of the function.

·        (1) Point will be awarded for setting the derivative equal to zero.

·        (1) Point will be awarded for the correct value of  c.

F:      Objective: Understand the Mean Value Theorem and the conditions under which it applies.

            If the MVT DOES NOT APPLY:

·        (1) Point will be awarded for correctly identifying that the MVT does not apply.

·        (1) Point will be awarded for proper mathematical work or a correct explanation that explains why the MVT does not apply.

If the MVT DOES APPLY:

·        (1) Point will be awarded for correctly identifying that the MVT does apply.

·        (1) Point will be awarded for calculating the average rate of change of the function on [a,b]: .

·        (1) Point will be awarded for finding the derivative of the function.

·        (1) Point will be awarded for setting the derivative equal to the average rate of change of the function on [a,b]

·        (1) Point will be awarded for the correct value of  c.

G.      Objective: Understand the graphical interpretation of the MVT

            If the MVT DOES NOT APPLY:

·        (2) Points will be awarded for correctly identifying the MVT does not apply.

·        (2) Points will be awarded for a proper mathematical explanation that explains why. (0) points will be awarded for a an explanation that is ambiguous, incomplete, or only partially correct.

If the MVT DOES APPLY:

·        (2) Points will be awarded for correctly identifying the MVT does apply.

·        (2) Points will be awarded for a tangent line that passes through a point for which the instantaneous rate of change is equal to the average rate of change. No partial credit shall be awarded. 

H.      Objective: Understand and apply the First Derivative Test

·         (1) Point will be awarded for finding all critical numbers of the function.

·         (1) Point will be awarded for using the first derivative test to determine changes in the sign of the derivative of the function.

·         (1) Point will be awarded for evaluating the function at the critical numbers.

·         (2) Points will be awarded for correctly identifying all relative extrema of the function. Partial credit of (1) point will be awarded for partially complete lists of extrema.

I.      Objective: Understand and Apply the Second Derivative Test

·         (1) Point will be awarded for finding all critical numbers of the function

·         (1) Point will be awarded for evaluating the function at the critical numbers.

·         (1) Point will be awarded for finding the second derivative of the function and evaluating the second derivative at the critical numbers.

·         (2) Points will be awarded for correctly identifying relative extrema of the function based on the results of the Second Derivative Test. Partial credit of (1) point will be awarded for partially complete lists of extrema.

J.      Objective: Use techniques of differentiation to extensively analyze a function.

 

Send mail to calcunderthestars@gmail.com with questions or comments about this web site.
Last modified: 01/09/08