3.7 Optimization

Download as Word Document

Practice Test: No Calculators Permitted in Parts A-C,E,F, G#19,20                                            

A. Find the linearization of the function at .

1.                                                2.

3.                                           4.

B. Find the differential dy of the function.

5.                                                                     6.

7.                                                           8.

C. Use differentials to estimate  for the specified value of () at .

9.                                  10.

D. Use differentials to estimate  for the given values of  and . Then compute the error, , for the approximation of  provided.

11.                       12.

E. Estimate the given number.

13.                                                                   14.

15.                                                                       16.

F. Find the point on the graph of the function closest to the specified point.

17.                                                       18.

G. Solve the following problems. A calculator is permitted/required for some of the problems of this section.

19. Find two numbers whose sum is 360 and whose product is a maximum.

20. Find two numbers whose product is 360 and whose absolute sum is a minimum.

21. A rectangular pen is to be made from 1500 m² of material. Find the dimensions of the pen that maximize the area.

22. Below is the graph of a function  and the line tangent to the graph of the function at . Determine from the graph, for each of the values of x () below, if dy is less than, greater than, or equal to the value of .

a)

b)

c)

23. Find the maximum area of a rectangle inscribed by the line , the x-axis, and the y-axis.

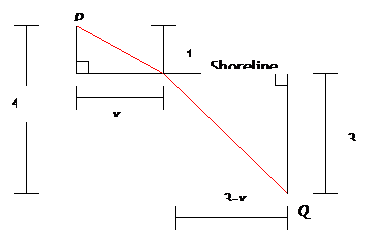
24. A box is to made from a sheet of cardboard, measuring 1 meter by 3 meters, by cutting four squares of equal area from the four corners of the sheet and folding the remaining material into a box. Find the dimensions of the box that maximize the volume.

25. Ricardo is rowing in a boat at point P 1 mile north of the horizontal shoreline. If he wishes to reach a point Q that is 3 miles east of his position and 4 miles south of his position, and if he can row at 2 mi/hr. and walk at 5 mi/hr., what path will minimize the time?

26. An engineer designs a spherical reservoir of radius 5 m to hold petroleum reserves. If the measurement of the radius of the reservoir is accurate within 0.005 m, estimate the maximum error in the calculation of the volume of the reservoir (The formula for the volume of a sphere is ).

27. A cylindrical tin can with a top is to be constructed from 60 m² of material. Find the dimensions of the can that will maximize the volume.

28. Find the maximum volume of a circular cone that can be inscribed within a circle of radius 5 m.

29. A rectangle is inscribed within the region bounded above by  and bounded below by , as shown in the figure below. Find the dimensions of the rectangle that maximize its area.

30. A woman stands at a point A in front of a circular lake of radius 4 km and wishes to reach a point C directly across the lake. She can row a boat at 4 km/hr and walk at a rate of 4 km/hr.

1. Draw a complete diagram (more than shown here) of the situation. Label all known angles and distances.
2. Write a formula for the distance (in km) of the woman’s path (shown in red) as a function of θ.
3. Given the information about how quickly the woman can row and how quickly she can walk, write a formula for the time of the woman’s path.
4. Minimize the time function from part (c) and describe the path that minimizes the time.

Solutions:

1.                                                         2.        

3.                                          4.        

5.                                                                                 6.        

7.                                                           8.        

9.                                  10.      

11.                       12.      

13.       Let .                                                      14.       Let

            Then                                                 Then         

15.       Let                                            16.       Let  (Note: )

            Then                                          Then

17.      

            Distance

            We wish to minimize the distance. It suffices to minimize the argument within the radical to determine where the minimum will occur, but we will minimize D to avoid confusion.

            D is minimized for . The closest point is .

18.      

            Distance

            We wish to minimize the distance. If suffices to minimize the argument within the radical

            to determine where the minimum will occur, but we will minimize D to avoid confusion.

            D is minimized when . The closest point is .

19.                       20.      

            P  is maximized when                     is minimized when

21.      

            A is maximized when

22.       a)                                     b)                               c)

23.       Since  and Area,

            .

            The maximum area of the rectangle is thus given by

24.                                                                                        

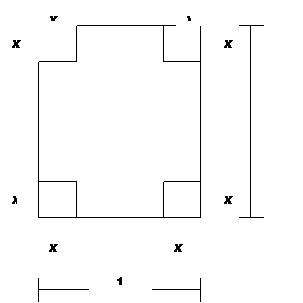
From the figure, we see that

The dimensions are

25.           From the figure, we can see that the distance is given by the following:

                Since , the time function is given by the following:

                Ricardo should proceed rowing to a point on the shore 0.279 miles east of his position

                and then proceed directly towards point Q to minimize time.

26.          

27.          

                The volume of the can is maximized when .

28.           The formula for the volume of a cone is .

                But from the figure, we see that    and  

                Thus,

                 ().

                The maximum volume is thus .

29.

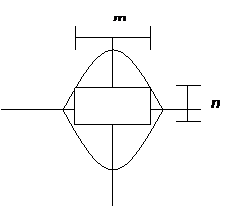
Let m be the width of the rectangle, given by . Let n be the height of the box, given by

. The area of the rectangle is thus given by the formula below:

(We are only considering positive x values)

Plugging that value of x into our equations for m and n, we obtain

The rectangle of maximum area thus has dimensions .

30.

a.

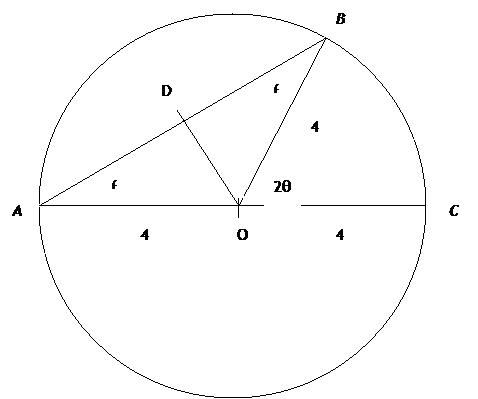
(Line segment OD is perpendicular to line segment AB)

b. From the figure above, we can see that the distance the woman must travel is the sum of the lengths of line segment AB and the arc BC. Thus, the formula for the distance of the woman’s path is given below:

c. Since , the time function is given below:

d.

Time is thus minimized if the woman rows at an angle  northward of point C.

Send mail to calcunderthestars@gmail.com with questions or comments about this web site.
Last modified: 01/09/08